Abstract

To improve the crashworthiness and energy absorption of thin-walled tube structures, a bionic thin-walled tube was designed based on the structural characteristics of antler osteon and the principle of structural bionics and had the same inner and outer diameters and the same gradient thickness as antler osteon. A nonlinear finite element method is used to simulate the crashworthiness of a thin-walled tube with equal gradient thickness variation (EGTTS) under axial and oblique loads. The crashworthiness of EGTTS-7 (Egtts with 7 layers) was evaluated using the complex proportional assessment(COPRAS). A multi-objective particle swarm optimization (MOPSO) algorithm was used to optimize the EGTTS-7 and the Pareto boundary was used to obtain the optimal structure parameters of the EGTTS-7 by using the loading angles of 0°, 10°, 20°, and 30°. It is found that the crashworthiness of the EGTTS is best when the axial load weight factor of the case is large. Compared with EGTTS and circular tubes(CT), F _max can be reduced by up to 50.1% and EA can be increased by up to 22.7%.

Keywords:
Thin-walled tube; Structural bionics; Crashworthiness design; COPRAS; MOPSO algorithm

Graphical Abstract

1. Introduction

Thin-walled tube structures are widely used as energy absorbers in the transportation, aerospace, shipping, and aircraft industries because of their high specific strength, high specific stiffness, and high energy absorption [¹[1] Baroutaji A, Sajjia M, Olabi A G. On the crashworthiness performance of thin-walled energy absorbers: recent advances and future developments. Thin-Walled Structures 2017; 118:137-163.

[2] Sun Y, Li Q M. Dynamic compressive behaviour of cellular materials: A review of phenomenon, mechanism and modelling. Int J Impact Eng 2018, 112: 74-115.

[3] Razaghi R, Sharavi M, Feizi MM. Investigating the effect of sloshing on the energy absorption of tank wagons crash. Transactions of the Canadian Society for Mechanical Engineering. 2015;39(2):187-200.-⁴[4] Supian A B M, Sapuan S M, Zuhri M Y M. Hybrid reinforced thermoset polymer composite in energy absorption tube application: A review. Defence Technology 2018; 14:291-305.] properties. Research on thin-walled tubes with traditional cross-sections has been conducted, such as on round tubes [⁵[5] Tai Y S, Huang M Y, Hu H T. Axial compression and energy absorption characteristics of high-strength thin-walled cylinders under impact load. Theoretical and applied fracture mechanics 2010; 53:1-8.-⁶[6] Wu Z, Shi L, Cheng X. Transverse impact behavior and residual axial compression characteristics of braided composite tubes: Experimental and numerical study. Int J Impact Eng 2020; 142:103578.], square tubes [⁷[7] Tang Z, Liu S, Zhang Z. Analysis of energy absorption characteristics of cylindrical multi-cell columns[J]. Thin-Walled Structures, 2013, 62: 75-84.-⁸[8] Li X, Xiao L, Song W. Deformation and failure modes of Ti-6Al-4V lattice-walled tubes under uniaxial compression. Int J Impact Eng 2019; 130:27-40.], rectangles [⁹[9] Baroutaji A, Morris E, Olabi A G. Quasi-static response and multi-objective crashworthiness optimization of oblong tube under lateral loading. Thin-Walled Structures 2014; 82:262-277.], polygons [¹⁰[10] Qiu N, Gao Y, Fang J, Feng Z, Sun G, Li Q. Crashworthiness analysis and design of multi-cell hexagonal columns under multiple loading cases. Finite Elements in Analysis and Design. 2015 Oct 15;104:89-101.-¹¹[11] Tarlochan F, Samer F, Hamouda A M S. Design of thin wall structures for energy absorption applications: Enhancement of crashworthiness due to axial and oblique impact forces. Thin-Walled Structures 2013; 71:7-17.], and polycells [¹²[12] Pirmohammad S, Marzdashti S E. Crushing behavior of new designed multi-cell members subjected to axial and oblique quasi-static loads. Thin-Walled Structures 2016; 108:291-304.-¹³[13] Kuleyin H, Gümrük R. Pressure wave propagation in pressurized thin-walled circular tubes under axial impact. Int J Impact Eng 2019; 130:138-152.]. Additional research results have been obtained about the mechanical properties and energy absorption characteristics of thin-walled tubes under lateral loading [¹⁴[14] Acar E, Altin MU, Güler MA. Evaluation of various multi-cell design concepts for crashworthiness design of thin-walled aluminum tubes. Thin-Walled Structures. 2019 Sep 1;142:227-35.

[15] Ataabadi P B, Karagiozova D, Alves M. Crushing and energy absorption mechanisms of carbon fiber-epoxy tubes under axial impact. Int J Impact Eng 2019; 131:174-189.

[16] Chen B C, Zou M, Liu G M. Experimental study on energy absorption of bionic tubes inspired by bamboo structures under axial crushing. Int J Impact Eng 2018; 115:48-57.-¹⁷[17] Zhang X, Zhang H. Static and dynamic bending collapse of thin-walled square beams with tube filler. Int J Impact Eng 2018; 112:165-179.]. Several scholars have added an induction structure to the traditional thin-walled tube structure in their research. L. Tan et al. [¹⁸[18] Tan L H, Xu T, Cui X M. Design optimization for crashworthiness of metal thin-walled cylinders with circular arc indentations. Explosion and Shock Waves 2014; 34:547-553.] have introduced an arc-shaped groove induction structure about a thin-walled metal tube and have produced a multi-objective optimization design to obtain betterenergy absorption.. Z. Yin [¹⁹[19] Yin Z P, Li Y L, Huang Q Q. Optimal crashworthiness design of thin-walled circular tubeswith triggering holes. Explosion and Shock Waves 2011; 31:418-422.] used least squares surface fitting and a genetic algorithm to optimize the crashworthiness of thin-walled round tubes with induced defects. The results show that the optimized structure has a high energy absorption effect and is convenient for application in structural designs. W. Hao et al. [²⁰[20] Liu Z, Hao W, Qin Q. Buckling and energy absorption of novel pre-folded tubes under axial impacts. Applied Physics A 2017; 123:351.] have introduced a fold structure about a square tube, have established the fold angle formula of the fold tube by using geometric relations, and have used LS-DYNA to study the buckling mode and energy absorption performance of various fold tubes. The results showed that the introduction of folds can effectively improve energy absorption performance and that the axial thickness of a thin-walled tube will also affect its crashworthiness. F. Xu et al. [²¹[21] Xu F X, Zhang S, Wu K Y. Study on crashworthiness design criteria and method of tubular structures withpower exponent distribution of thickness. Explosion and Shock Waves 2019; 39:135-143.] have studied a thin-walled energy-absorbing structure in which the tube wall thickness is continually distributed in the form of a power exponent. The design criteria for crashworthiness of the tube are given and the quantitative analysis of other tube structures under equal mass conditions is derived based on the distribution characteristics. The relationship is analyzed and the impact of various gradients on the crashworthiness of power exponent tubes is evaluated. Eyvazian et al. [²²[22] Eyvazian A, Najafian S, Mozafari H. Crashworthiness analysis of a novel aluminum bi-tubular corrugated tube-experimental study//Advances in manufacturing processes. Springer, Singapore, 2019: 599-607.] have designed a new type of double bellows and conducted a compression test to evaluate crashworthiness under radial loading conditions, which effectively enhanced the energy absorption of thin-walled pipes under radial loading and produced more energy than a uniform tube does. G. Li et al. [²³[23] Li G, Xu F, Sun G. A comparative study on thin-walled structures with functionally graded thickness (FGT) and tapered tubes withstanding oblique impact loading. International Journal of Impact Engineering 2015; 77:68-83.] have analyzed the functionally graded thickness under oblique impact load and the energy absorption of a tapered tube and have shown that the gradient index 2.0 has an increased energy absorption effect. Menouer et al. [²⁴[24] Menouer A, Baleh R, Djebbar A. New generation of energy dissipating systems based on biaxial buckling. Thin-Walled Structures 2014; 85:456-465.] have studied biaxial buckling of copper and aluminum alloy circular tubes (CT) and square tubes under oblique loading. They have shown that an increase in the angle increases the rate of change of the torsional component and the average crushing force.

Natural organisms have evolved over a long period of time to adapt to their environments and have produced optimized processes for hunting and self-defense [²⁵[25] Huo P, Xu S C, Fan X W. Oblique impact resistance of a bionic thin-walled tube based on antles osteon. Explosion and Shock Waves 2020; 11:127-138.]. Biomimetic thin-walled tubes exhibit excellent structural crashworthiness when their mechanical properties are applied to the design of thin-walled tubes. Based on a bionic prototype of the structure of the odontodactylus scyllarus, a bionic unit multi-cell thin-walled tube was designed and its impact resistance under axial and oblique impact was studied. The structural parameters were optimized using MOPSO and the optimal solution was obtained [²⁶[26] Yang X, Fan X W, Xu S C. Design and crashworthiness analysis of thin-walled tube based on shrimp chela structure. Explosion and Shock Waves 2020; 40:62-72., ²⁷[27] Huang H, Xu S. Crashworthiness analysis and bionic design of multi-cell tubes under axial and oblique impact loads. Thin-Walled Structures 2019; 144:106333.]. A thin-walled tube composed of a bionic section, bionic unit, and bionic inner tube was designed by applying a bamboo section to the thin-walled tube [²⁸[28] Xu S C, Zou M, Wei C G. Axial crashworthiness analysis and optimization of a bionic thin-walled tube based on bamboo structure. Journal of Tsinghua University (Science and Technology) 2015; 54:299-304., ²⁹[29] Zou M, Xu S, Wei C. A bionic method for the crashworthiness design of thin-walled structures inspired by bamboo. Thin-Walled Structures 2016; 101:222-230.]. J. Chen [³⁰[30] Yu X, Pan L, Chen J. Experimental and numerical study on the energy absorption abilities of trabecular-honeycomb biomimetic structures inspired by beetle elytra. Journal of Materials Science 2019; 54:2193-2204.] and J. Du [³¹[31] Hao P, Du J. Energy absorption characteristics of bio-inspired honeycomb column thin-walled structure under impact loading. Journal of the mechanical behavior of biomedical materials 2018; 79:301-308., ³²[32] Xiang J, Du J, Li D. Numerical analysis of the impact resistance in aluminum alloy bi-tubular thin-walled structures designs inspired by beetle elytra. Journal of Materials Science 2017; 52:13247-13260.] have observed the microstructures of the hollow column and pole tube of the ladybug coleoptera and have proposed the bionic trabecular-honeycomb thin-walled structure, the bionic honeycomb thin-walled structure, and the bionic double-tube thin-walled structure, as well as having studied the mechanical properties of bionic structures under axial impact loads. In this paper, a new type of tubular wave structure is proposed to simulate the contours of the coconut tree. Four deformation modes of the bionic tube exist, which are affected by the cone angle and wavelength, and exhibit a significantly lower initial peak crushing force than a CT does.

In addition to the above biological prototypes, various studies have found that antlers also have high strength and excellent mechanical properties [³³[33] San Ha N, Lu G, Xiang X. High energy absorption efficiency of thin-walled conical corrugation tubes mimicking coconut tree configuration. International Journal of Mechanical Sciences 2018; 148:409-421.]. Antlers are a status symbol and act as weapons and shields during stag fights, showing extremely high strength, toughness, and bending resistance [³⁴[34] D. Currey, John. Bones: structure and mechanics, Princeton university press, US, 2006.]. Antlers can withstand impact loads much higher than the mass of a male deer and are able to endure bending and avoid fracturing [³⁵[35] Lincoln G A. Biology of antlers. Journal of Zoology 1992; 226:517-528.]. Kitchener et al. [³⁶[36] Henshaw J. Antlers-the unbrittle bones of contention. Nature 1971; 231:469-469.] have studied various types of antlers and have found that the specific strength of antlers was higher than that of mild steel and have determined that antlers can resist deformation. Mechanical tests on antlers performed by Chen et al. [³⁷[37] Kitchener A. The effect of behaviour and body weight on the mechanical design of horns. Journal of Zoology 1985; 205:191-203.] have shown that the axial strength of antlers was approximately 197.3 MPa, which was higher than that of the transverse strength (approximately 66.7 MPa). Z. Fang et al. [³⁸[38] Chen P Y, Stokes A G, McKittrick J. Comparison of the structure and mechanical properties of bovine femur bone and antler of the North American elk (Cervus elaphus canadensis). Acta Biomaterialia 2009; 5:693-706.] have studied the microstructure of densified antler osteon and have tested the bending mechanical properties of three specimens by using a material testing machine. The crack growth path and fracture morphology from bending in three different directions were observed using a scanning electron microscope. The antlers have anisotropic mechanical properties, showing that the unique structure of antler osteon has a significant effect on the mechanical properties of antler.

Based on the structural bionic principle, a new bionic thin-walled tube with EGTTS is designed according to the microstructure characteristics of antler osteon, the energy absorption under axial and oblique loading is studied using nonlinear finite element analysis, and crashworthiness is investigated. The parameters of the bionic thin-walled tube are also optimized using MOPSO to obtain the structural parameters for a tube with the best crashworthiness, which can be used in the design and application of the thin-walled tube.

2. Bionic design of thin-walled tube

2.1. Microstructure characteristics of antler bone

Osteon is also called the Haversian system [³⁹[39] Fang Z, Chen B, Lin S. Investigation of inner mechanism of anisotropic mechanical property of antler bone. Journal of the Mechanical Behavior of Biomedical Materials 2018; 88:1-10.], which is the primary structural unit of antlers and other dense long bones, as shown in Fig. 1. The osteon is cylindrical and its outer diameter increases layer by layer, with its axis parallel to the long axis of the long bone. Each osteon has 4 layers to 20 layers of concentric annular tubes and the height of each layer is identical, the thickness decreases from bottom to top, and the gradient of thickness changes is identical [³⁷[37] Kitchener A. The effect of behaviour and body weight on the mechanical design of horns. Journal of Zoology 1985; 205:191-203., ⁴⁰[40] Sun J J, Geng J. Mechanical Properties of human compact bone. Advances In Mechanics 1987; 17:200-215.].

Similarity analysis showed that the load and function characteristics of osteon are similar to those of thin-walled tubes, which can withstand axial loads, oblique loads, and lateral loads when impacted. When a thin-walled tube is subjected to an impact load in different directions, the resulting collision energy can be absorbed by deformation. Antler osteon also has this function and is an excellent bionic prototype for designing bionic thin-walled tubes.

2.2. Bionic thin-walled tube design

Based on the principle of structural bionics, a thin-walled tube of EGTTS was designed by analyzing the microstructure of osteon and simulating its multilayer structure (the inner diameter was identical, the outer diameter decreased from bottom to top, and the gradient phase of wall thickness changed). The dimensions of EGTTS are height h = 160 mm, outer diameter D ₁ = 70 mm, and inner diameter D ₂ = 66 mm. The number of bionic layers are N = 2, 3, 4, 5, 6, 7, 8, 9, and 10. Various suffixes are used to differentiate different numbers of bionic layers of EGTTS. For example, EGTTS-2 represents an EGTTS with two layers, as shown in Fig. 2. The figure provides the front view of EGTTS with different numbers of bionic layers. EGTTS with different bionic layers are given different gradient values to ensure that the mass of each EGTTS is 0.15 kg.

2.3. Establishment and verification of EGTTS finite element model

The finite element models of the above nine EGTTS are established using HyperMesh software. The aluminum alloy AA6061 is chosen as the material, with initial yield strength σ _y = 250 MPa, elastic modulus E = 71 GPa, density ρ = 2.7 × 10³kg/m³, and Poisson’s ratio μ = 0.3. A bilinear elastic-plastic material with strain hardening characteristics is adopted and the corresponding material tab in HyperMesh is MATL24. The mass and velocity of the moving rigid wall are 200 kg and 10 m/s, respectively, and the loading angle θ is 0°, 10°, 20°, and 30°, respectively. A fixation constraint is applied to the bottom of the EGTTS, which is fixed on a rigid base. The EGTTS finite element model under axial and oblique impact loads is shown in Fig. 3.

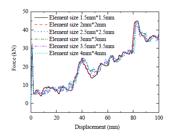
The EGTTS finite element model of five different grid elements is simulated and the numerical results are shown in Fig. 4. The error between element 1.5 mm × 1.5 mm and element 2.0 mm × 2.0 mm is smaller, which shows that the smaller mesh size cannot significantly improve the accuracy of numerical simulation results, but that computational complexity will increase significantly. Finally, the 2.0 mm × 2.0 mm mesh size was used.

An EGTTS-4 specimen with biomimetic layer n = 4, gradient a = 0.22, height h = 160 mm, outer diameter D ₁ = 70 mm, inner diameter D ₂ = 66 mm, and bottom layer thickness t = 4 mm was fabricated. Impact tests were performed to verify the finite element model of the specimen, as shown in Fig. 5.

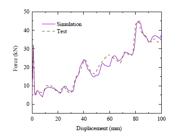
The impact force can be recorded by a drop weight sensor and the deformation process can be recorded using a high-speed video camera. The crushing force versus displacement curve of EGTTS-4 is shown in Fig. 6. The stress-displacement relationship of the simulation is generally consistent with experimental values and the deformation mode of the simulation agrees with the experimental results. The relative errors between simulation and test results are 3.76% for maximum crushing force, 6.08% for energy absorption, and 5.28% for crushing force efficiency. Therefore, the finite element model established in this paper has sufficient accuracy and can be used for further comparative analysis and design optimization of different types of EGTTS thin-walled tubes.

3. Numerical simulation results of EGTTS

3.1. Crashworthiness index

To correctly evaluate the crashworthiness of EGTTS, it is necessary to determine an appropriate crashworthiness index. Most literature uses F _max, EA, and CFE to evaluate the crashworthiness of thin-walled tubes [¹[1] Baroutaji A, Sajjia M, Olabi A G. On the crashworthiness performance of thin-walled energy absorbers: recent advances and future developments. Thin-Walled Structures 2017; 118:137-163.].

F_max represents the maximum crushing force of the thin-walled pipe, which should be reduced as much as possible during the deformation process. An excessively large F _max value will cause excessive acceleration, that is, a large impact force will cause greater damage to a device using thin-walled pipes.

EA represents the energy absorption of the thin-walled tube during the deformation process, which can be expressed by Eq. (1).

In the formula, x is the deformation displacement and F(x) is the instantaneous crushing force under this displacement.

CFE represents the crushing force efficiency, which can be expressed by Eq. (2).

In the formula, F _mean is the average crushing force, which is the ratio of EA to x, which can be expressed by Eq. (3).

3.2. Crashworthiness analysis of EGTTS

The deformation modes of EGTTS with different numbers of bionic layers under axial and oblique impact loads are shown in Fig. 7. EGTTS exhibits a stable and progressive crush pattern under multi-angle impact loads. As the angle increases, an overall bending mode appears at the bottom of the EGTTS, but the overall deformation is stable and there is no direct overall bending.

EGTTS-4 is shown in Fig. 8 as an example of the difference in crushing force-displacement curves at different impact angles. For axial loading, the crushing force first reaches a peak, then drops sharply, then fluctuates at various lower values corresponding to the progressive fold and a new peak appears at the change of deformation to thickness, but is smaller than the peak of the initial crushing force. The appearance of the curve is caused by a sudden change in thickness. After the new peak appears, the curve continues to change in a progressive way until it reaches its maximum value. The collapse of the fold occurs when the critical condition of deformation is reached. For oblique loading, the peak value of the crushing force is small; beyond the peak value, the curve fluctuates at the maximum value and no new peak value appears. The maximum crushing force under axial loading is larger than that under oblique loading. The position of the maximum crushing force increases with the increase of the loading angle θ.

The maximum crushing force F _max, energy absorption EA, and crushing force efficiency CFE of different biomimetic layers are shown in Fig. 9. Because F _mean represents the ratio of energy absorption to displacement, it is not listed here. The maximum value of F _max is 44.97 kN in EGTTS-4 under axial loading. The EA gap and the change were small, with the highest value of 1.65 kJ being at EGTTS-9.

Under oblique loading, both F _max and EA decrease, but CFE increases. At 10° and 20° loading, the decrease of F _max is larger than that of EA, which results in CFE being larger than that of axial loading at oblique loading and higher than that at 20° loading. Increasing the loading angle to 20° and 30° shows no obvious change in F _max, but a decrease in EA, which leads to the decrease in CFE compared with 20°.

3.3. Optimal thin-walled tube structure selection

Based on the above three crashworthiness evaluation indices, the thin-walled tube structures with the best crashworthiness were selected from the nine EGTTS with different layers. In this paper, the complex proportional assessment (COPRAS) is used to solve the multi-objective decision-making problem.

Step 1: Generate the decision matrix A, which is applied with the EGTTS crashworthiness index of nine different layers under four loading angles.

In this formula, a _ij is the value of the i scheme under the index j, m is the number of design schemes, this paper refers to the number of bionic layers, and n is the number of indicators.

Step 2: Obtain the normalized decision matrix R in order to obtain the dimensionless values under different indices for comparison.

Step 3: Determine the individual weights for each indicator, as follows.

In this paper, the total comparison set is C = n(n-1)/2 = 3. Using the scaling method [¹⁸[18] Tan L H, Xu T, Cui X M. Design optimization for crashworthiness of metal thin-walled cylinders with circular arc indentations. Explosion and Shock Waves 2014; 34:547-553.], two comparisons are made and crashworthiness indices are scaled according to their importance, as shown in Table 1. Sum the w _j of index j as shown in Eq. (6) and then calculate the weight of the j index w _j , as with Eq. (7).

In this paper, the criterion Wa under multi-angle loading is considered. The weight factors of the loading angle are 0.4(θ = 0°), 0.3(θ = 10°), 0.2(θ = 20°), and 0.1(θ = 30°), respectively. For example, when F _max is weighted, the weighting factors should be 0.417 × 0.4 = 0.1668(θ = 0°), 0.417 × 0.3 = 0.1251(θ = 10°), 0.417 × 0.2 = 0.0834(θ = 20°), and 0.417 × 0.1 = 0.0417(θ = 30°), respectively.

Step 4: Compute the weighted normalized decision matrix D.

From Eq. (8), d _ij is the weighted normalized index value of the i scheme under the j index. All EGTTS crashworthiness indices under different loading conditions are taken into account when the decision matrix is generated, as shown in Table 2.

Step 5: Sum the weighted normalized values of the beneficial and non-beneficial attributes.

In the formula, d _+ij and d _-ij are weighted normalized performance values for beneficial and non-beneficial attributes, respectively.

Step 6: Determine the relative merits of the different options.

where Q _i is the value of relative superiority. The higher the Q _i value is, the higher the superiority of the scheme is.

Step 7: Calculate the utility of scenario i.

where Q _max is the maximum value of relative excellence. The larger the value of the utility U _i , the better the crash resistance of the design, and a value of 100% corresponds to the optimal structure. The relative merits of each scenario, Q _i and the utility U _i , are shown in Table 3. The results show that when the number of biomimetic layers is n = 7, the utility is the highest, that is, the crashworthiness of EGTTS-7 is the best considering various loading angles. The structural parameters are further optimized in the following section.

4. Multi-objective optimization

4.1. Optimization model

To obtain the optimal crashworthiness of EGTTS, its structural parameters are optimized; this paper uses a multi-objective optimization design under different loading conditions. Energy absorption is the primary function of a thin-walled tube, which is expected to absorb as much energy as possible. Therefore, EA is an optimization target; F _max should also be used as an optimization target because too large an F _max may cause the impact height to decelerate and cause serious injury or death to vehicle passengers. In addition, the impact of different loading angles should also be considered. Therefore, this paper expresses the weighted index as Eq. (13). F _max,w and EA _w , respectively, represent the weighted maximum crushing force and the weighted energy absorption value. k represents the number of loading conditions; in this paper k = 4 and I = 1, 2, 3, and 4 represent the loading angle θ = 0°, 10°, 20°, and 30°, respectively.

Based on the two weighted normalization indices F _max,w and EA _w , EA is maximized while F _max is minimized. For each loading angle θ, the optimization model can be expressed as Eq. (14).

4.2. Experimental design and meta-model

Because of the homogeneity of the sample points, the whole factor experiment is used to generate the sample points, and 25 sample points are generated. Polynomial regression (PR) was used to establish the meta-model of crashworthiness indices F _max and EA and the accuracy of the meta-model was determined according to R ². R ² is listed in Table 4. The results show that the prediction accuracy of the PR meta-model for crashworthiness indices F _max and EA is high and both R ² are close to 1, which indicates that the PR meta-model can be used in subsequent multi-objective optimizations.

4.3. Multi-objective optimization design

To solve the multi-objective optimization problem in Eq. (14), MOPSO is used to obtain the Pareto boundary and apply it to the optimization design. The weight factors w _a1 , w _a2 , w _a3 , and w _a4 were set for four loading angles: θ = 0°, 10°, 20°, and 30°. The impact of different loading angles on the crashworthiness of the thin-walled tube is studied by considering the following seven configurations. Case-I, case-II, case-III, and case-IV are four single-angle configurations. Case-V, case-VI, and case-VII are multi-angle configurations. The angle weighting factors for different configurations are shown in Table 5.

Based on the PR meta-model, the Pareto boundary is obtained as shown in Fig. 10. The maximum crushing force F _max and energy absorption EA decrease with the increase of the angle and F _max decreases with the decrease of the EA. However, when EA decreases in case-I, F _max decreases the most; when EA decreases in case-II, F _max decreases the least. When EA decreases in case-III and case-IV, the degree of F _max decrease is not obvious. This shows that the loading angle influences the position and range of the Pareto boundary, thus affecting its crashworthiness. During axial loading, the degree of change of F _max is close to that of EA, while under diagonal loading, the degree of change of F _max is different from that of EA.

To select the optimal structure for crashworthiness under four single-angle loading conditions, the minimum distance method is used to find the inflection point. The corresponding structural parameters are listed in Table 6.

The Pareto boundary of the scenario is configured for multiple loading angles, as shown in Fig. 10b. Case-V, case-VI, and case-VII move from the lower right-hand corner to the upper left-hand corner with little difference in the slope of the boundary because as the weight factor from case-V to case-VII increases, a larger F _max and EA are obtained. Case-VII absorbs more energy than case-VI and case-VI absorbs more energy than case-V under the same F _max. From the extension of the Pareto boundary, the thin-walled tubes under case-VII have better energy absorption than case-V and case-VI do. The selection of the thin-walled tube with the best crashworthiness is influenced by the weight factor when considering the different loading angles The weight factor should be considered comprehensively in practical application.

5. Crashworthiness comparison

The optimized EGTTS is simulated under the condition of single-angle loading and compared with the CT tube under the same condition to analyze crashworthiness. The same aluminum alloy is selected as the material for the CT. The initial yield strength is σ _y = 250 MPa, the elastic modulus is E = 71 GPa, the density is ρ = 2.7 × 10³ kg/m³, the Poisson's ratio is μ = 0.3, the mass is 0.15 kg, the height is 160 mm, and the thickness is the same as the optimized bottom layer thickness t of EGTTS in Table 6. Fig. 11 shows the comparison of EGTTS and CT numerical simulation results under four single loading angles. The optimized EGTTS has a lower F _max than the CT does and the optimized EGTTS with a thickness of 2.02 mm and a gradient of 0.15 mm reduces the F _max by 50.1% at a 20° oblique loading. Compared with the CT, the optimized EGTTS has a higher EA and the EGTTS with a wall thickness of 1.91 mm and a gradient of 0.13 mm under a 10° oblique loading can improve EA by 22.7%, which indicates that the optimized EGTTS has better crashworthiness.

6. Conclusion

Acknowledgments

This present work was supported by National Natural Science Foundation of China (Grant No. 51305223), Postdoctoral Research Foundation of China (Grant No. 2018M641338) and Agriculture Research System of China (Grant No.CARS-27).

References

Edited by

Editor:

Publication Dates

History